使用牛顿法求解立方根

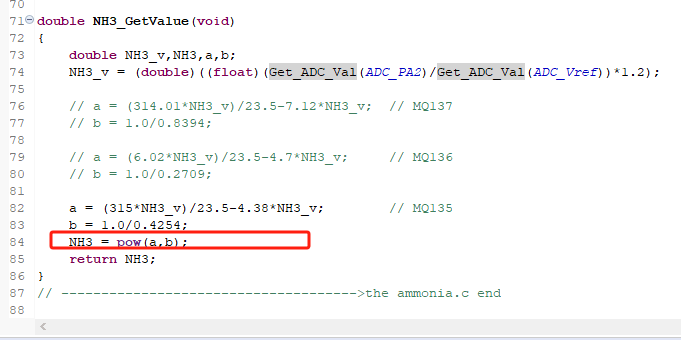
前些天有位群友问了这个问题：不用库求解上图中的NH3。

pow()函数是C语言中的库函数，用于求幂。观察可知，b约为2.35，差不多就是 $2\frac{1}{3}$，在精度要求不那么特别高的情况下，可以用 $a * a * \sqrt[3]{a}$ 来得到近似值，那问题就变成了求 a 的立方根。

牛顿法（Newton’s method）是一种用于求解方程根的迭代算法。它可以用于许多数学问题，包括计算立方根。本文将详细讲解如何使用牛顿法求解立方根，并通过示例进行说明。

牛顿法简介

牛顿法基于泰勒级数展开，通过迭代的方法逐步逼近函数的根。对于一个函数$f(x)$，假设我们已经有了一个初始猜测$x_0$，牛顿法的迭代公式为：

$$
x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}
$$

这里，$f’(x)$是函数$f(x)$的导数。

立方根的定义

我们想要找出一个数$a$的立方根$\sqrt[3]{a}$，这可以转化为求解方程：

$$
f(x) = x^3 - a = 0
$$

对这个方程求导，可以得到：

$$
f’(x) = 3x^2
$$

牛顿法求解立方根的步骤

结合上述信息，我们可以将牛顿法应用于求解立方根，具体步骤如下：

1. **选择初始值$x_0$**：选择一个接近$\sqrt[3]{a}$的初始猜测值。
2. 迭代计算：使用牛顿法公式进行迭代，直到满足精度要求：
   $$
   x_{n+1} = x_n - \frac{x_n^3 - a}{3x_n^2}
   $$
3. 停止条件：当$|x_{n+1} - x_n| < \epsilon$时，停止迭代（其中$\epsilon$是设定的精度）。

示例：求解$\sqrt[3]{27}$

我们来演示如何使用牛顿法求解 $\sqrt[3]{27}$。

1. 选择初始值：
   我们可以选择 $x_0 = 9$ 作为初始值。

2. 迭代过程：
   进行迭代计算，直至达到所需精度。

   • 第一次迭代：
     $$
     x_1 = 9 - \frac{9^3 - 27}{3 \times 9^2} = 9 - \frac{729 - 27}{243} = 9 - \frac{702}{243} \approx 6.111
     $$
   • 第二次迭代：
     $$
     x_2 = 6.111 - \frac{6.111^3 - 27}{3 \times 6.111^2} \approx 4.297
     $$
   • 第三次迭代：
     $$
     x_3 = 4.297 - \frac{4.297^3 - 27}{3 \times 4.297^2} \approx 3.419
     $$
   • 第四次迭代：
     $$
     x_4 = 3.419 - \frac{3.419^3 - 27}{3 \times 3.419^2} \approx 3.048
     $$
   • 第五次迭代：
     $$
     x_5 = 3.048 - \frac{3.048^3 - 27}{3 \times 3.048^2} \approx 3.001
     $$
   • 第六次迭代：
     $$
     x_6 = 3.001 - \frac{3.001^3 - 27}{3 \times 3.001^2} \approx 3.000
     $$

   经过几次迭代后，我们可以看到结果逐渐逼近 3，满足精度要求。

代码实现

下面是用 Python 实现牛顿法求解立方根的代码示例：

def cubic_root(a, epsilon=1e-7):
    # 初始猜测值
    x_n = a / 3.0  # 可以选择 a 的一个近似值
    while True:
        x_n1 = x_n - (x_n**3 - a) / (3 * x_n**2)  # 牛顿法迭代
        if abs(x_n1 - x_n) < epsilon:  # 停止条件
            break
        x_n = x_n1
    return x_n

# 测试
result = cubic_root(27)
print(f"立方根 27 的结果是：{result}")

总结

牛顿法是一种高效的求解方程根的方法，尤其适合用于计算立方根。通过合理选择初始值和迭代公式，我们可以快速得到精确的结果。希望本文对你理解牛顿法求解立方根有所帮助！

有什么更好的方法，欢迎在下方留言！